Biography
I am a Statistician and Data Scientist at the Department of Clinical Science, Lund University, Lund, Sweden. My work focuses on developing probabilistic predictive tools that combine computational, experimental, and clinical methods in medical science. I am also researching the structural comparison of proteins and the genetic variations in disease-related biological pathways.
Previously, I was a research fellow in Statistical Machine Learning at André Lab in the Center for Molecular Protein Science, Lund University, where I explored probabilistic models in protein modeling and prediction. Before that, I served as a tenure-track assistant professor of Statistics at the Department of Statistics in Shiraz University and Persian Gulf University between 2015 and 2019.
I have collaborated extensively with Biologists, Medical Physicians, Epidemiologists, Physicists, and Computer Scientists to translate interdisciplinary challenges into computational frameworks. My research interests include statistical machine learning, directional statistics, non-parametric modeling, and Bayesian statistics, with applications in bioinformatics, neuroimaging, and the sustainable development of AI systems to understand complex systems.
This website will take you to my recent research papers and reports, teaching material, external activities, and blog posts. You are welcome to contact me if you are interested in connecting.
Download my resumé.
- Statistical Machine learning
- Directional Statistics
- Bayesian Modeling
- Non-parametric Modeling
PhD in Statistics, 2015
Shahid Beheshti University
Msc in Mathematical Statistics, 2010
Tarbiat Modares University
BSc in Statistics, 2008
Persian Gulf University
Skills
100%
100%
100%
Experience
Responsibilities include:
- Taught Advanced R and C++ Programming, Statistical Modeling and Simulation Studies, Probability, and Linear Algebra courses (70%).
- Researching Statistical Machine Learning and Directional Statistics (30%)
- Member of entrepreneur and innovation committee
Responsibilities include:
- Analysing
- Modelling
- Deploying
- Strategic Planing
- Project Management
Responsibilities include:
- Taught Statistical Bayesian Modeling, Simulation Studies, Probability, Statistical Mehtods, and Linear Algebra courses (70%).
- Researching Statistical Machine Learning and Directional Statistics (30%)
- President’s Management Advisory Board member in Statistics and Strategic Planning
Featured Publications
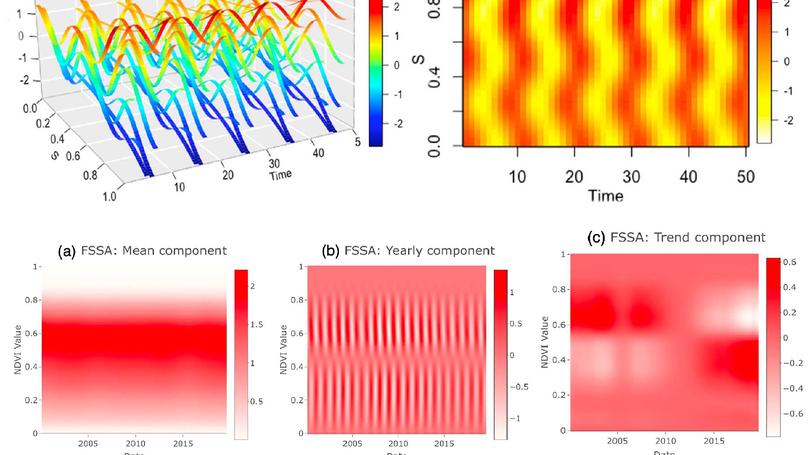
In this paper, we develop a new extension of the singular spectrum analysis (SSA) called functionalSSA to analyze functional time series. The new methodology is constructed by integrating ideasfrom functional data analysis and univariate SSA. Specifically, we i ntroduce a trajectory operatorin the functional world, which is equivalent to the trajectory matrix in the regular SSA. In theregular S SA, one needs to obtain the singular value decomposition (SVD) of the trajectorymatrix to decompose a given time series. Since there is no procedure to extract the functionalSVD (fSVD) of the trajectory operator, we introduce a computationally tr actable algorithm toobtain the fSVD components. The effectiveness of the proposed approach is illustrated by aninteresting example of remote sensing data. Also, we develop an efficient and user-friendly Rpackage and a shiny web application to allow interactive exploration of the results.
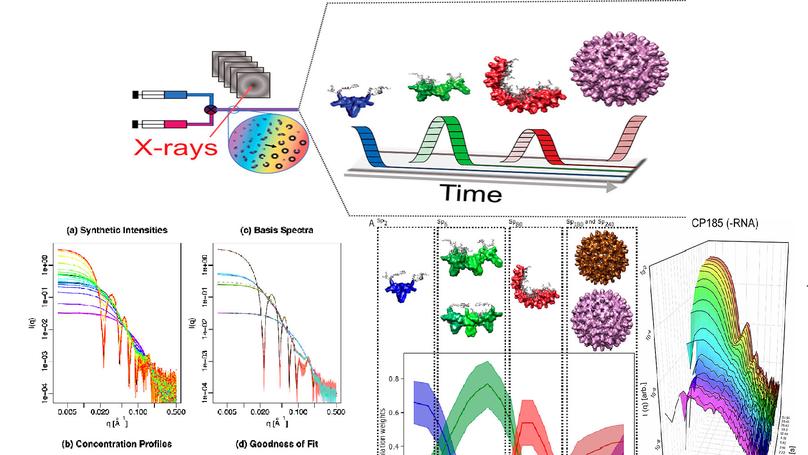
Copyright © 2020 American Chemical Society. The genetic material of viruses is protected by protein shells that are assembled from a large number of subunits in a process that is efficient and robust. Many of the mechanistic details underpinning efficient assembly of virus capsids are still unknown. The assembly mechanism of hepatitis B capsids has been intensively researched using a truncated core protein lacking the C-terminal domain responsible for binding genomic RNA. To resolve the assembly intermediates of hepatitis B virus (HBV), we studied the formation of nucleocapsids and empty capsids from full-length hepatitis B core proteins, using time-resolved small-angle X-ray scattering. We developed a detailed structural model of the HBV capsid assembly process using a combination of analysis with multivariate curve resolution, structural modeling, and Bayesian ensemble inference. The detailed structural analysis supports an assembly pathway that proceeds through the formation of two highly populated intermediates, a trimer of dimers and a partially closed shell consisting of around 40 dimers. These intermediates are on-path, transient and efficiently convert into fully formed capsids. In the presence of an RNA oligo that binds specifically to the C-terminal domain the assembly proceeds via a similar mechanism to that in the absence of nucleic acids. Comparisons between truncated and full-length HBV capsid proteins reveal that the unstructured C-terminal domain has a significant impact on the assembly process and is required to obtain a more complete mechanistic understanding of HBV capsid formation. These results also illustrate how combining scattering information from different time-points during time-resolved experiments can be utilized to derive a structural model of protein self-assembly pathways.
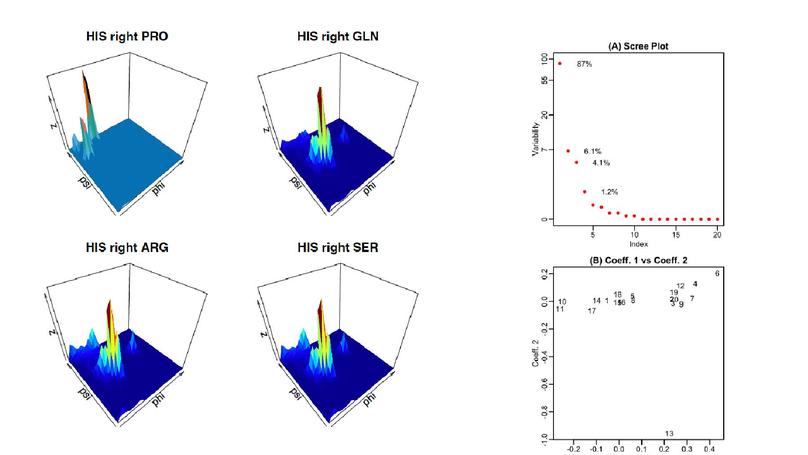
We considered the circular nature of the angular data using trigonometric spline, which was more efficient than the triangulation technique. This general framework also provides comprehensive machinery for clustering, model assessment, or data modeling for groups of protein backbone angles. Specifically, the estimated angular density corresponding to a protein structure has a basis expansion whose coefficients can be used as an input to a clustering algorithm. Furthermore, most of the existing protein classification techniques use sequence and 3D structure comparison to classify the proteins based on some (dis)similarity scores obtained after pairwise alignments. The proposed method is an alignment-free procedure that provides a vector of coefficients (i.e., features) associated with each structure (density) that can be directly used to classify the proteins. This general framework also provides a comprehensive means for assessing clustering models for various other data groups with circular nature. We also developed a shiny web application available at https://pscde-t.shinyapps.io/PSCDE-T/) that can be used by the research community to reproduce the results in this paper and estimate Ramachandran distributions collectively
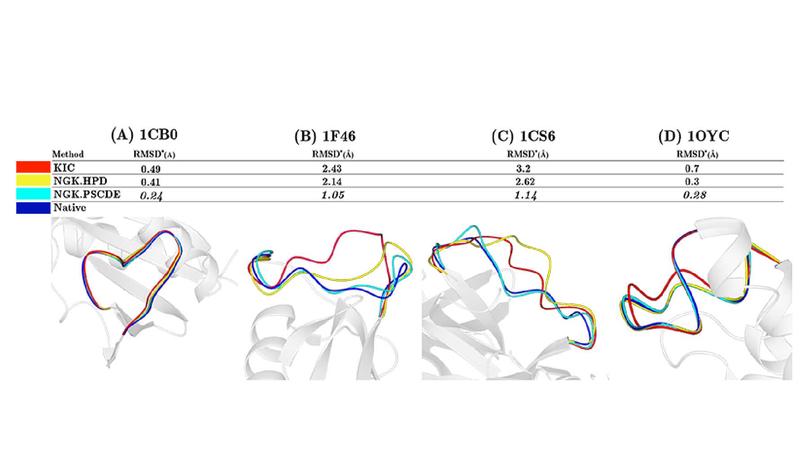
© 2016 American Statistical Association. This article develops a method for simultaneous estimation of density functions for a collection of populations of protein backbone angle pairs using a data-driven, shared basis that is constructed by bivariate spline functions defined on a triangulation of the bivariate domain. The circular nature of angular data is taken into account by imposing appropriate smoothness constraints across boundaries of the triangles. Maximum penalized likelihood is used to fit the model and an alternating blockwise Newton-type algorithm is developed for computation. A simulation study shows that the collective estimation approach is statistically more efficient than estimating the densities individually. The proposed method was used to estimate neighbor-dependent distributions of protein backbone dihedral angles (i.e., Ramachandran distributions). The estimated distributions were applied to protein loop modeling, one of the most challenging open problems in protein structure prediction, by feeding them into an angular-sampling-based loop structure prediction framework. Our estimated distributions compared favorably to the Ramachandran distributions estimated by fitting a hierarchical Dirichlet process model; and in particular, our distributions showed significant improvements on the hard cases where existing methods do not work well.
Contact
- morteza.najibi--at--med.lu.se
- (+46) 76 160 5054
- Kioskgatan 3, SUS, Lund, Scåne 222 42
- DM Me on Twitter








